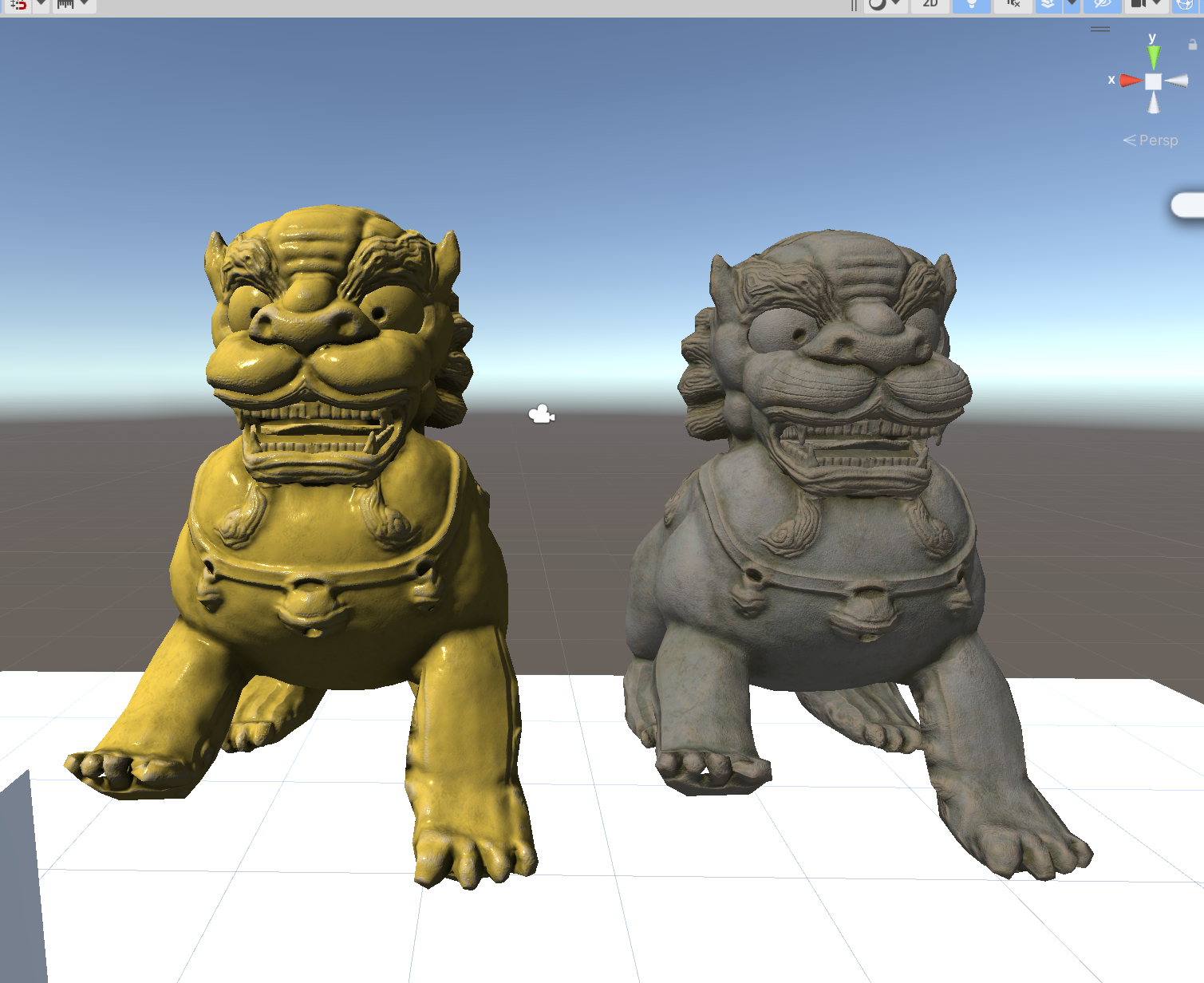
unity 实现 PBR
— 敖立鑫
前置知识
unity shder 几种渲染模式

这里使用前向渲染管线
通过在 Tags中添加 “LightMode” = “ForwardBase” 选择渲染模式
ForwrdBase
- 基础光照计算:漫反射,镜面反射,阴影计算等
- 考虑所有光源
- 计算平行光
ForwrdAdd
- 额外的光照效果:逐像素的操作
- 默认计算 前四个最重要的 点光源
这里我们只用一个平行光,暂时只用 ForwrdBase
搭建场景
首先新建一个场景,使用 hdrp 管线
替换 material

实现
先实现一个 blinn-phong 光照模型
因为我们要实现更好的效果,不考虑性能,所以我们的光照计算都将在 frag shader 进行
首先新建一个 unlitShader

添加 pbr
理论
有多种 brdf 模型
我们这里主要实现 Cook-Torrance BRDF
Cook-Torrance BRDF 分为漫反射和镜面反射两个部分
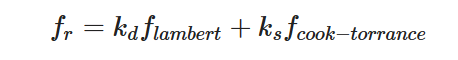
漫反射采用 lambertian 漫反射,

镜面反射主要有三个函数
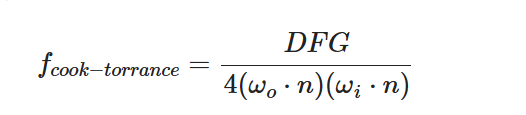
- D 法线分布函数:表示反射光强度在法线附件的分布,微平面向量和面法向越接近,强度越大。通过粗糙度改变波瓣形状
- 近似表示了微平面与半程向量的一致的比率
- G 几何函数:表示掠视时的几何遮蔽,通过史密斯法叠加入射和出射两个方向
- F 菲涅尔方程:表示菲涅尔效应,掠视金属时反射较多的光而俯视时反射光较少
CG 实现
法线分布函数
// 法线分布函数
// 法线,半程向量,粗糙度
float D_GGX_TR( fixed3 N, fixed3 H, float a)
{
float a2 = a * a;
float NdotH = max(dot(N,H),0);
float NdotH2 = NdotH * NdotH;
float nom = a2;
float denom = ( NdotH2 * (a2 - 1.0) + 1.0 );
denom = PI * denom * denom;
return nom / denom;
}
// 几何方程
float GeometrySchlickGGX(float NdotV, float roughness )
{
float r = (roughness + 1.0);
float k = (r*r) / 8.0;
float num = NdotV;
float denom = NdotV * (1.0 - k) + k;
return num / denom;
}
float GeometrySmith(fixed3 N, fixed3 V, fixed3 L, float roughness)
{
float NdotV = max(dot(N, V), 0.0);
float NdotL = max(dot(N, L), 0.0);
float ggx1 = GeometrySchlickGGX(NdotV, roughness);
float ggx2 = GeometrySchlickGGX(NdotL, roughness);
return ggx1 * ggx2;
}
// 菲涅尔方程
// cosTheta -- Normal dot viewDir F0 -- 表面颜色,反射率
fixed3 fresnelSchlick(float cosTheta , fixed3 F0)
{
return F0 + (1.0 - F0) * pow(clamp(1.0 - cosTheta, 0.0, 1.0) , 5.0);
}
效果不太好,以后有时间再优化